溃坝问题研究主要以历史资料统计分析及数值模拟为主，而溃坝在数值分析领域也成为了一个十分经典的案例，本文将使用积鼎 通用流体仿真软件VirtualFlow 模拟二维的溃坝流动。

案例描述

案例详情

1. 几何建模

本案例为二维算例，其中计算域的长为3.22m，高1.8m，水相的长为1.2m，高为0.6m，位于计算域左下角。同时在计算域底部距左端2.725m处设置监测点H1监测自由液面的高程，具体的几何和计算域如图 1.1所示。

图 1.1几何与计算域示意图

2. 网格划分

网格划分现有一套网格，网格一在x方向划分成161份，增长率为1，尺寸上限为1，最小尺寸为0.02m；y方向划分成90份，增长率为1，尺寸上限为1，最小尺寸为0.02m；z方向划分为1份，增长率设为1，比尺上限设为1，最终网格总数为14490，具体参数可见表 1.1。网格一划分的示意图如图 1.2所示。

表 1.1 网格信息表

注：括号内的数字分别对应网格划分份数、增长率和比尺上限

图 1.2 网格划分示意图

3. 参数设置

其中材料属性如表 1.2所示

表 1.2 材料属性

对于各边界的类型和具体边界条件如表 1.3所示。

表 1.3 边界条件

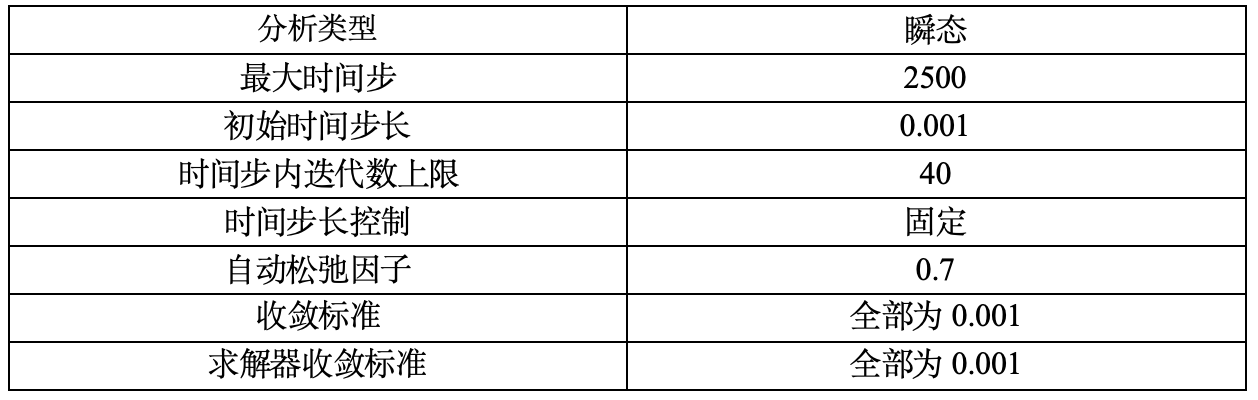
求解过程的参数设置和停止条件见表 1.4。

表 1.4 求解参数和停止条件

初始场的设置如表 1.5所示。

表 1.5 初始场设置

多相流模型使用Level-set模型参数为默认值。

数值模拟结果

本次将选择与Andrea Colagrossi和Maurizio Landrini[1]文章中使用SPH方法所做数值模拟的结果作对比如图1.3所示。

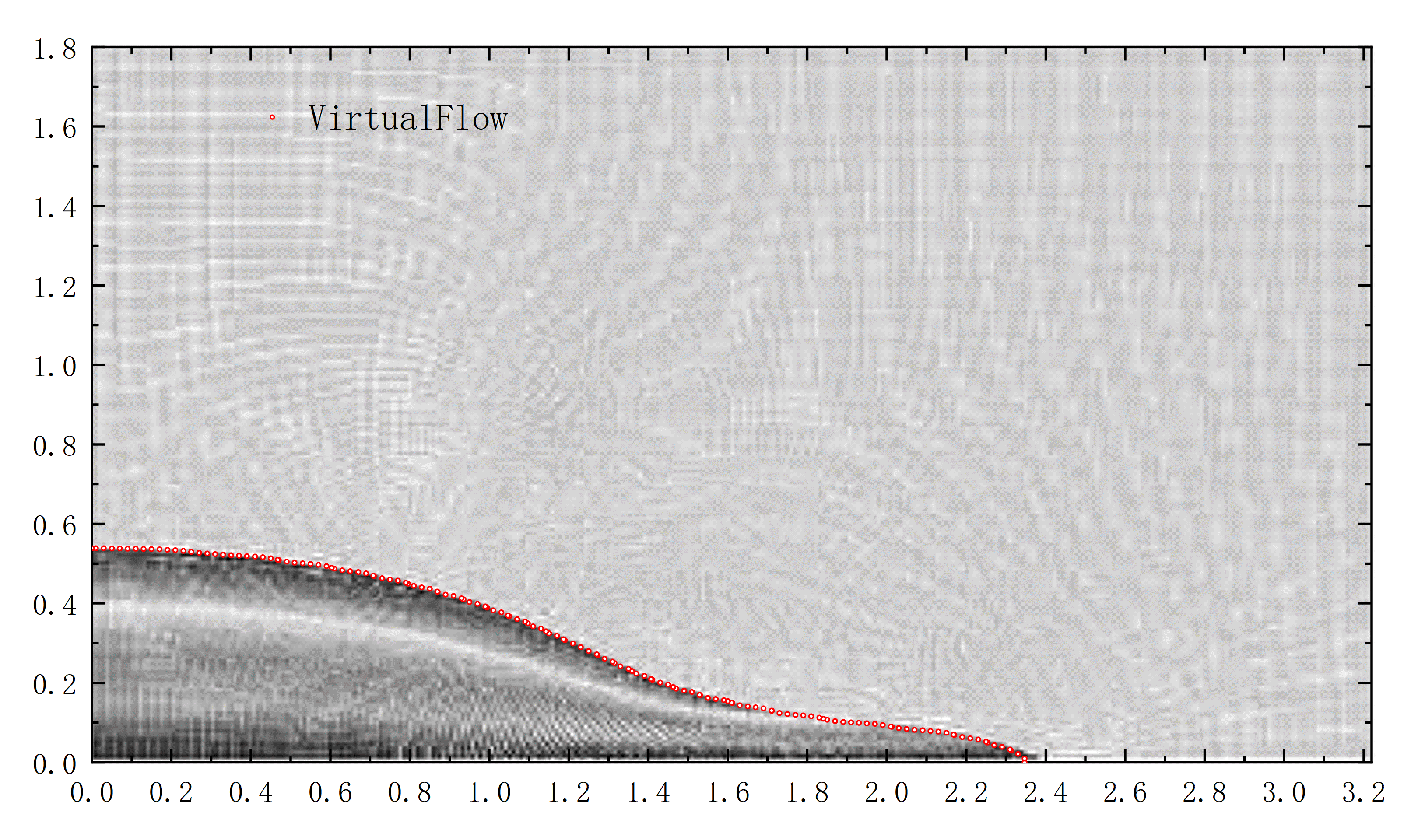
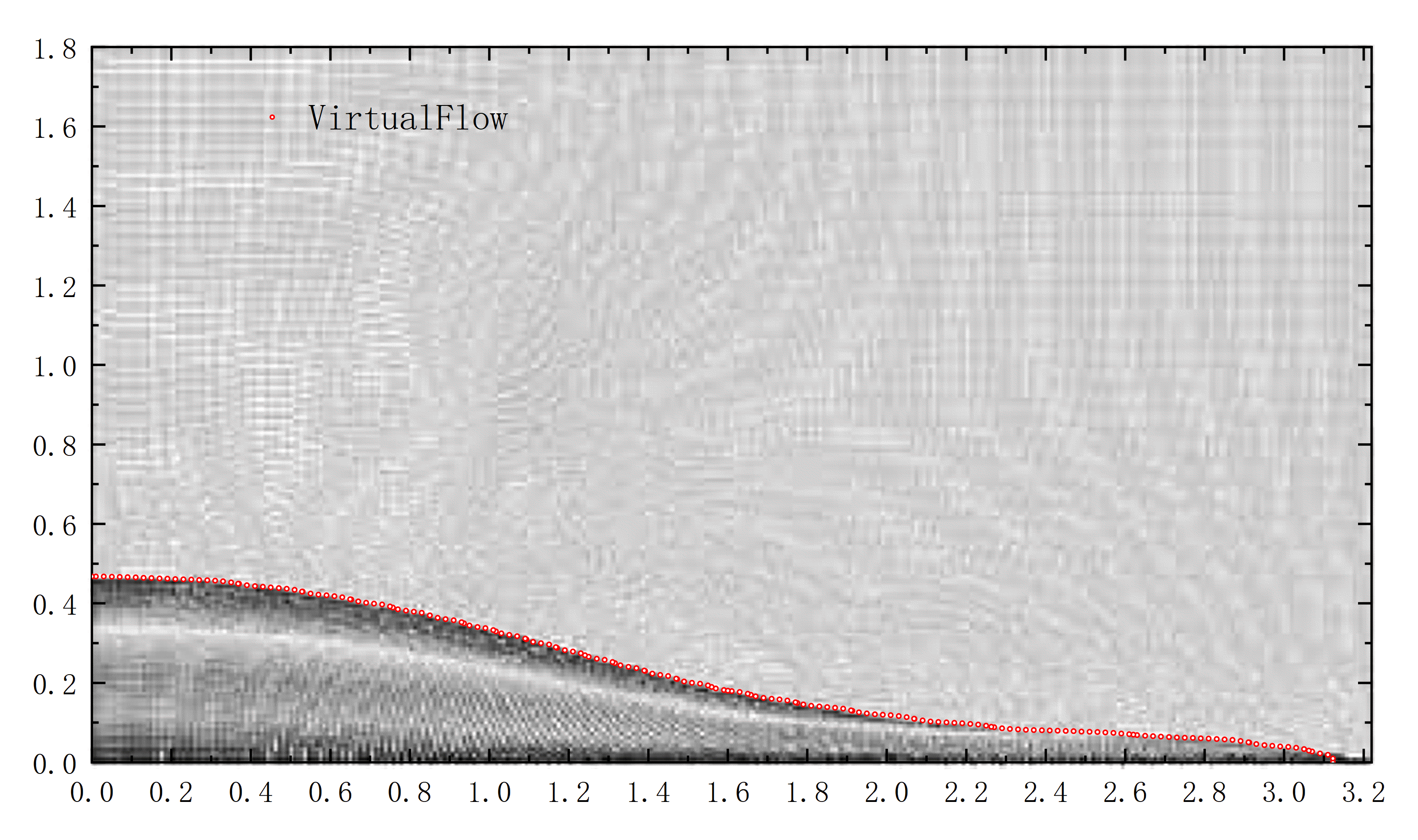
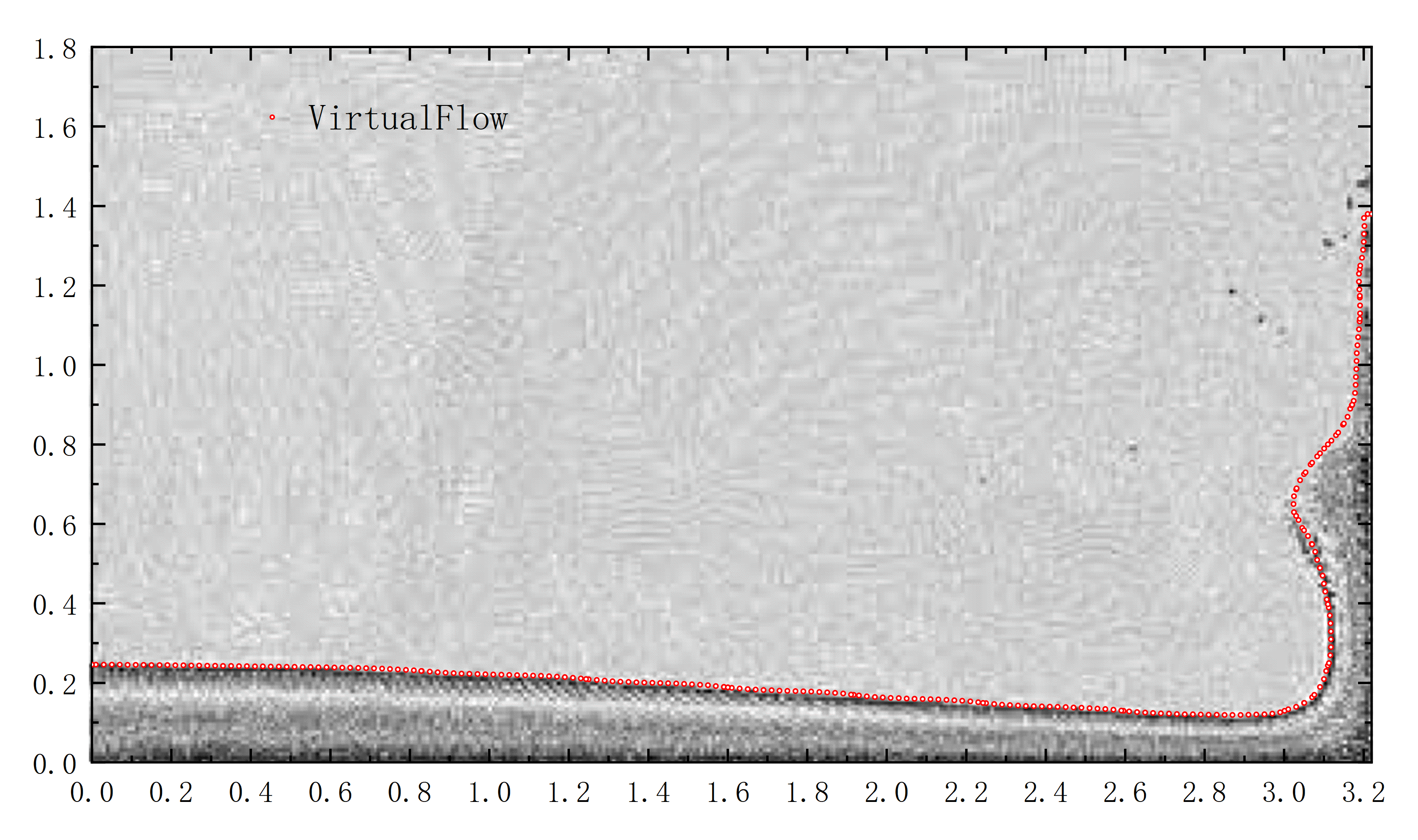
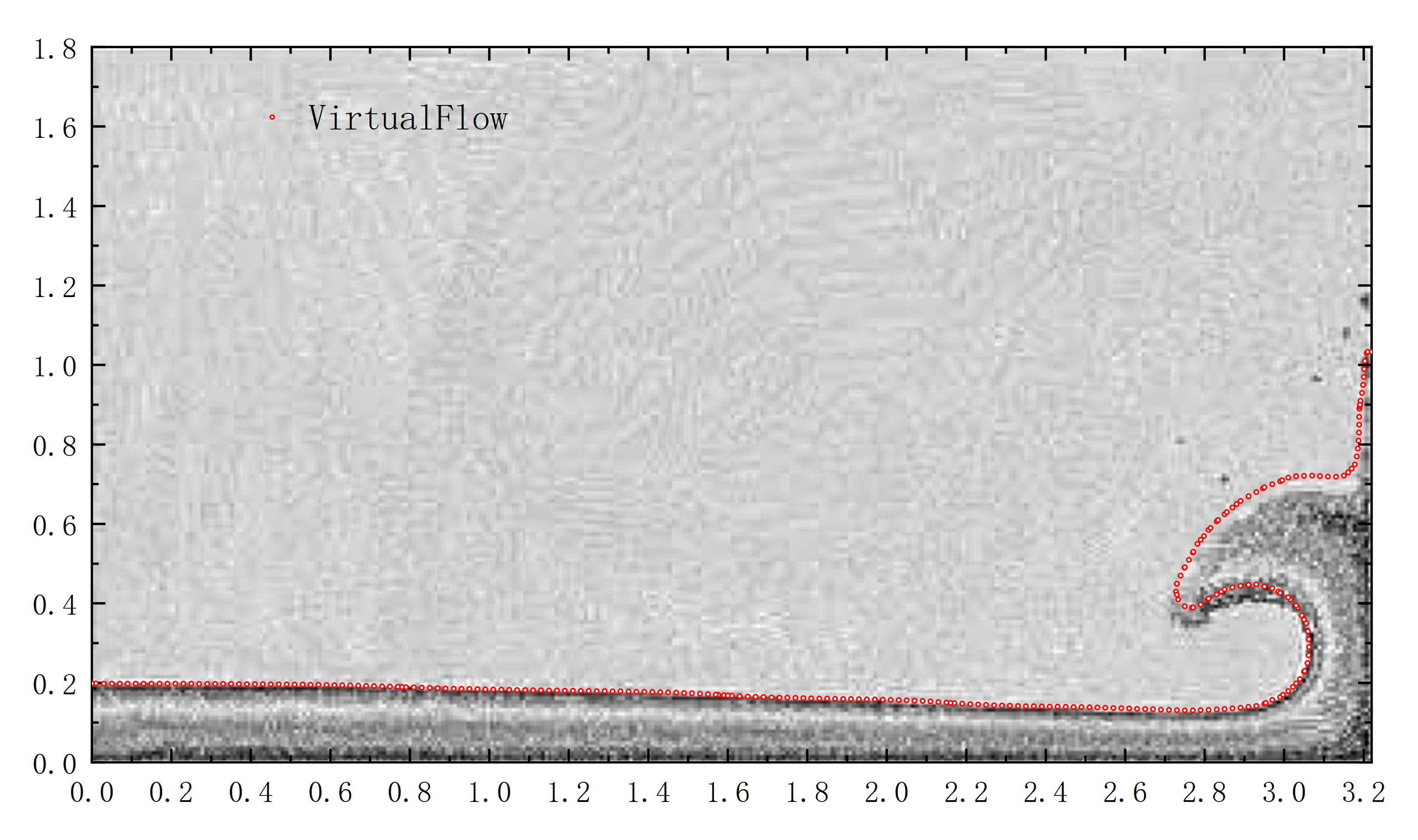
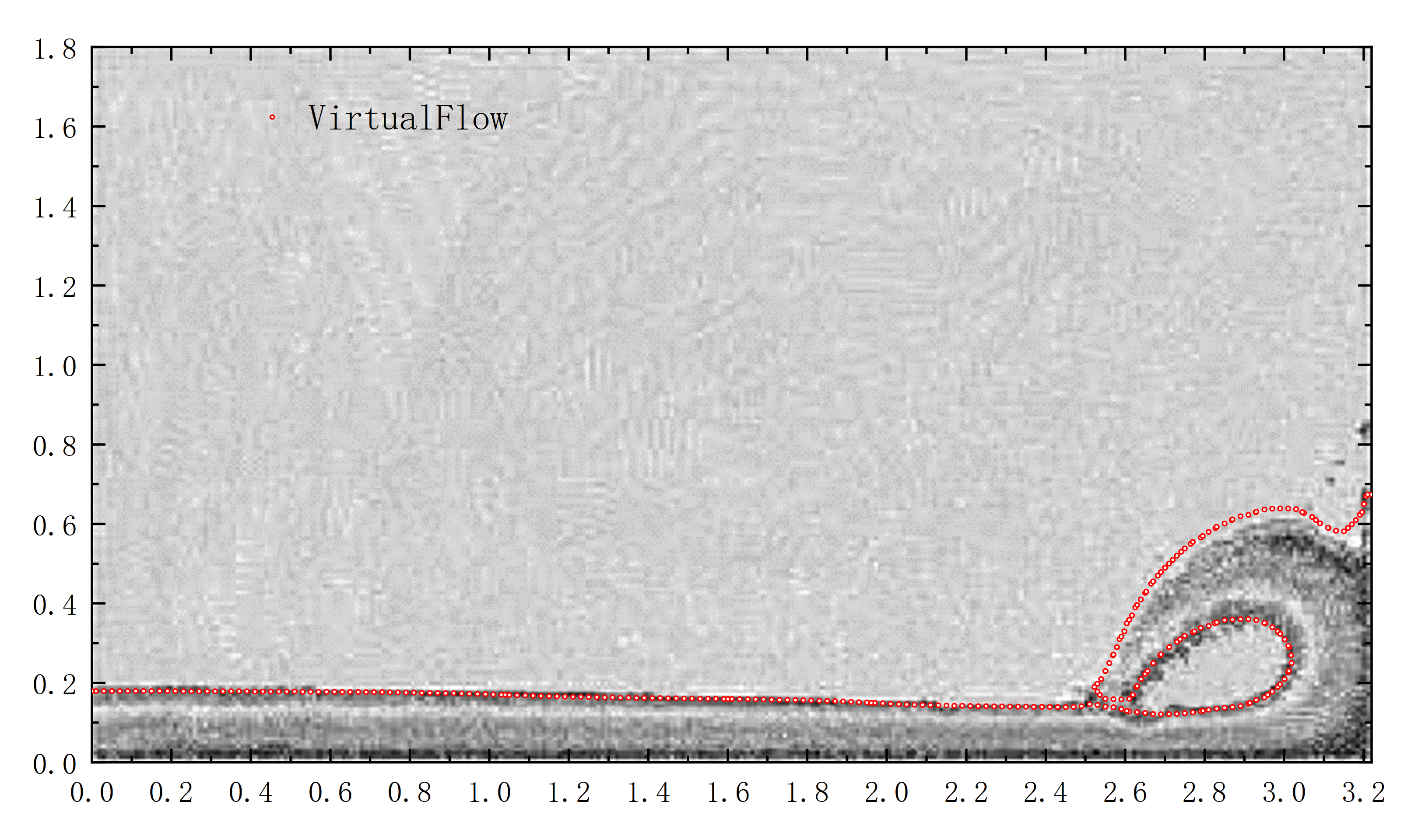
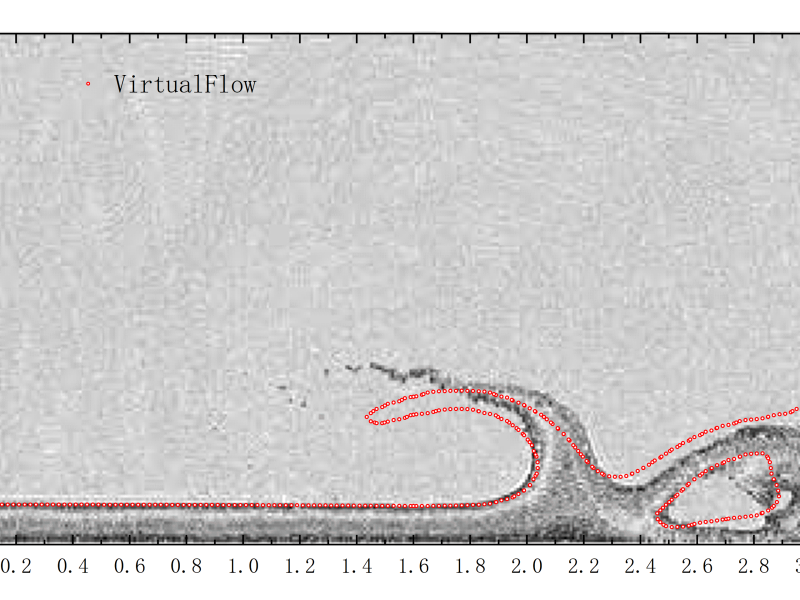
图 1.3 VirtualFlow与Andrea Colagrossi等人结果对比图

将H1监测点的结果与Andrea Colagrossi等人SPH方法的结论和Zhou[2]等人的试验测量值的对比结果如图1.4所示。

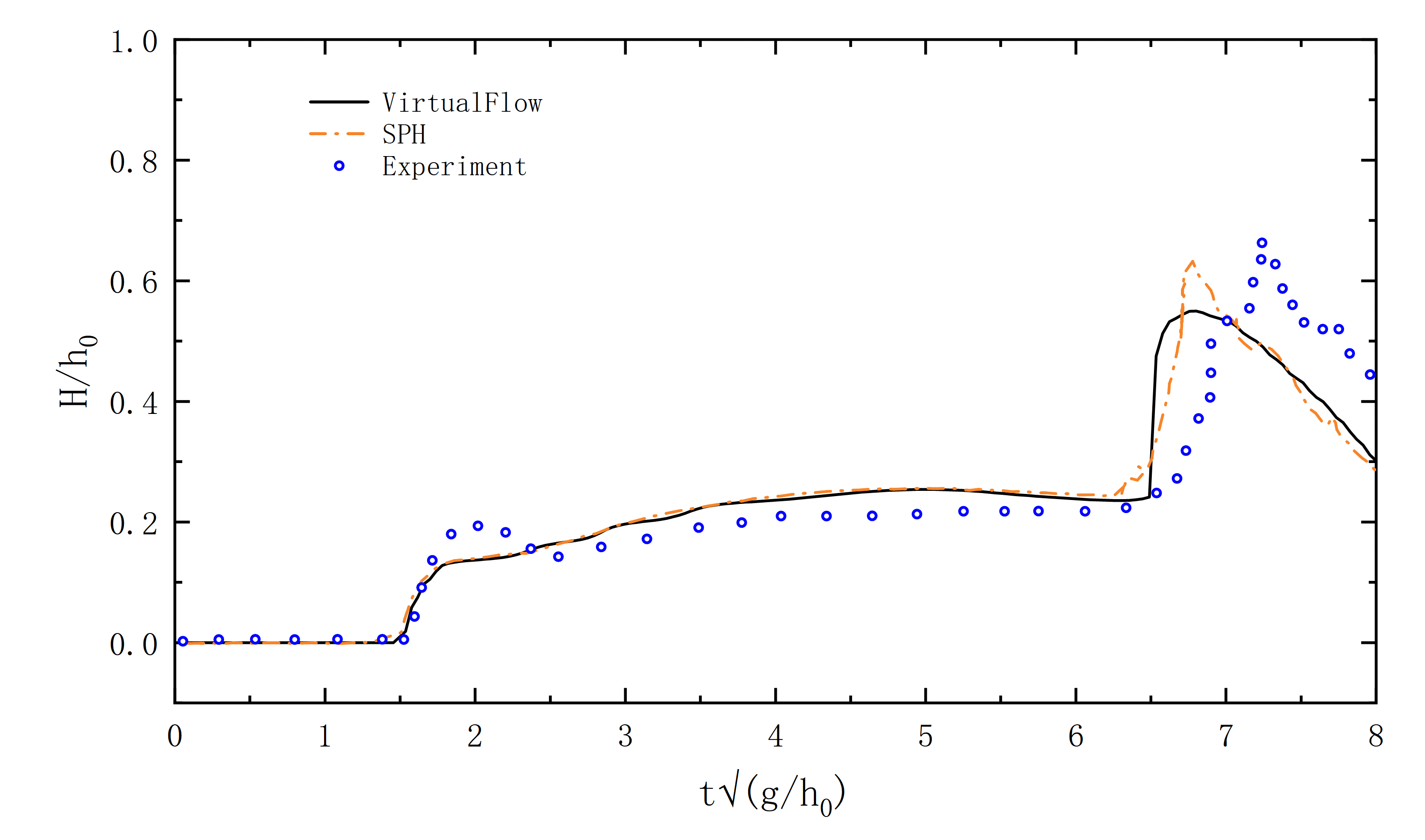
图 1.4 H1监测值对比图

总结

VirtualFlow软件准确模拟了二维溃坝水流的发展。从上述图中可以看出VirtualFlow计算的自由液面与Colagrossi等人用SPH方法计算的结果吻合良好；并且H1监测点的监测数据也与SPH方法和试验数据吻合，表明VirtualFlow处理计算界面流的可靠性。

参考文献

[1] COLAGROSSI A, LANDRINI M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics[J/OL]. Journal of Computational Physics, 2003, 191(2): 448-475. DOI:10.1016/S0021-9991(03)00324-3.

[2] ZHOU Z, DE KAT J, BUCHNER B. A nonlinear 3-D approach to simulate green water dynamics on deck[J]. 1999.