13162025768
免费试用
水下航行器(UUV)作为一种海洋探测装备,具备体积小、隐身性好、机动性强、成本低和可组网等优点。这些特点使得它们在海洋探索、科学研究、军事侦察等领域发挥着重要作用,其在现代海洋探测和军事领域中占据着越来越重要的地位。
水下航行器在航行时,会受到水流的阻力,其在航行过程中的阻力性能会影响其快速性, 水下航行器的快速性是评价其综合航行性能的一项重要战术技术指标。随着各种反潜设备的发展,水下航行器的航行安全问题不容忽视,提高航行器的快速性已经成为各国重要的军事研究课题,因而对其阻力的预报精度也有了更高的要求,suboff潜艇作为一种常见的水下航行器模型,曾在国际上被各大海洋强国进行充分的实验与数值模拟研究,本文以suboff模型对水下航行器阻力计算展开介绍。
在本研究中,在数值模拟中主要考虑的模型为全附体 SUBOFF 模型(配置8)[1]。设计的 CAD 模型的尺寸如图1所示。SUBOFF 模型是一个轴对称船体,总长度为 4.356 m,等直段最大直径 D 为 0.508 m。SUBOFF 型号在船体上方有一个舰桥,其前缘位于距船头 0.924 米(1.820D)处,后缘距离 1.293 米(2.545D),因此舰桥的总长度为 0.368 米(0.724D)。船尾有四个相同的附件,呈“十”字形布置(垂直和水平控制平面)。
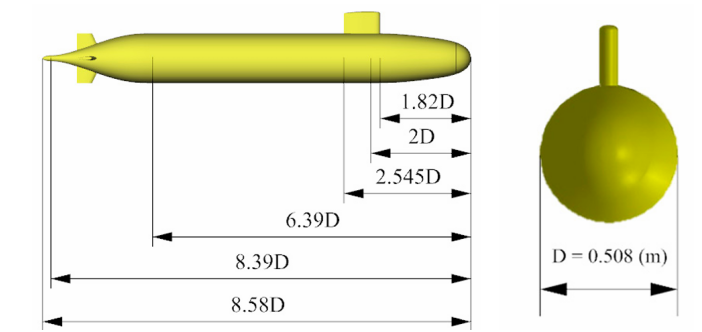
图 1 具有完全附体suboff潜艇模型/侧视图(左)和正视图(右)
在本研究中,数值模拟的湍流雷诺数均在107以上,采用了RANS方程求解,其以笛卡尔张量形式书写的连续性和动量方程分别如下:

其中,ρ 是体积分数平均密度;u 是流动速度,可以分解为均值 和波动分量u’;p 是压力项;μ 是动力粘度。
方程(2)中的最后一项表示湍流的影响,称为雷诺应力。基于 Boussinesq 假说 [2] 的雷诺应力与平均速度梯度相关,能够以如下公式给出:
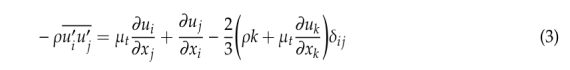
其中,μt表示湍流粘度,k表示动能,在湍流求解时,需选择合适的湍流模型,以构建μt和k相关的湍流封闭方程。
潜艇在深水区的潜航实际上是一个典型的绕流问题,对于绕流问题以及关于阻力问题的求解,一般采用的湍流模型为SST k-ω湍流模型,然而在关于该问题的求解中,采用可实现的k-ε模型较SST k-ω湍流模型所得计算结果与实验值吻合得更好,这可能是流动雷诺数较大引起的。
在计算过程中选取的计算域如下图 2所示(实际计算时采用半模计算)。计算域被设计为圆柱形,确保流动场的长度适合捕捉流动场特征,例如在任何速度下潜体后面的尾流效应。数计算域的长度设置为23.96米(约为艇长长度的5.5倍,即5.5L)。Moon等人[37]指出,对于潜体的CFD建模,流动场的宽度和高度可以设置为其直径的七倍(7D)。换句话说,如果计算域的高度和宽度都设置为模型直径的19倍(19D),数值流动场的模拟结果将进一步确保不受计算域边界的影响。同时图3显示了速度入口与压力出口(B.C.1和B.C.4)作为流体域两端的进/出口边界条件。同时,在外部流体区域的外边界上确定了自由滑移壁(B.C.2)。为了考虑粘性流动对刚体的影响,无滑移壁边界条件(B.C.3)应用于内部流体区域中的潜体表面。
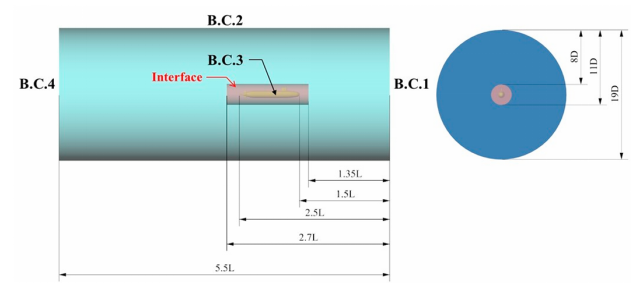
图 2 计算域的侧视图(左)和前视图(右)
对于CFD仿真过程中的网格收敛性问题,分别采用了五套不同的网格参数进行计算验证,表 1给出了五套不同网格的计算结果,可以发现给定的五套网格计算结果的最大偏差在0.6%,最终选用的网格为网格3,图 3给出了艇体壁面网格、艇体附近对称面以及围壳前缘的壁面网格示意简图。
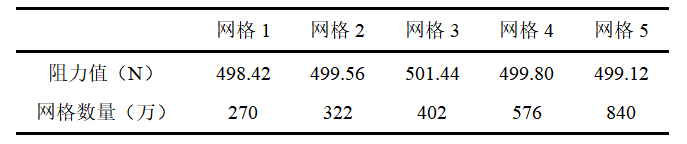
表 1 网格收敛性验证
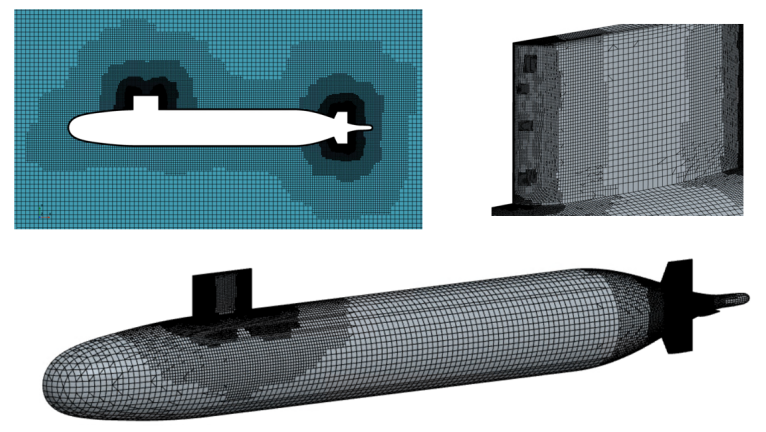
图 3 网格示意简图
图 4给出了各不同航速下,计算值与实验值的对比图,具体数据可见表 2,可以发现各航速下计算值均比实验值偏小,最大偏差在5%以内。
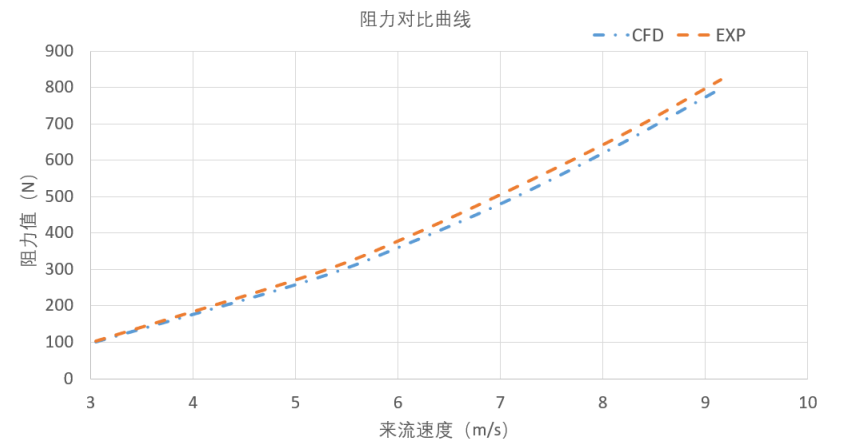
图 4 计算值与实验值对比曲线
表 2 计算值与实验值数据对比
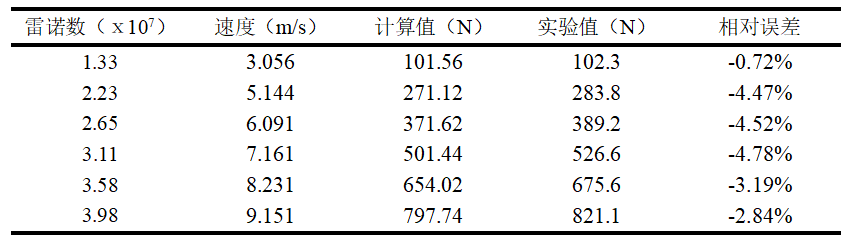
图 5给出了不同航速下,艇体上的压力分布以及中心对称面上的速度分布,从图中不难发现,航行速度的变化对淹没艇体周围的压力分布影响不大。压力最高的区域是艇体头部、围壳的前缘和尾舵的前缘。此外,在流速加快的地方,如艇体头部、围壳和尾舵附近,观察到了低压区,而在中部区域没有明显的压力变化。
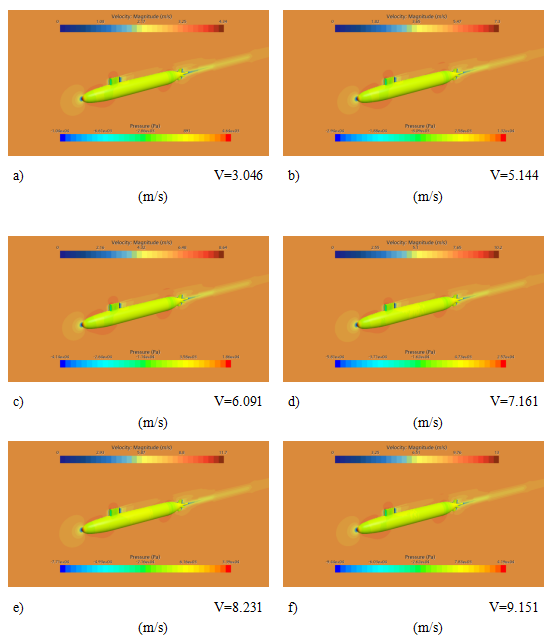
图 5 不同航速下,艇体上的压力分布以及中心对称面上的速度分布
潜艇水面附近的自航可以分为水面下自由航行与水面上自由航行,其区别为艇体部分是否存在裸露于空气中的部分,其计算域如下图 6所示。
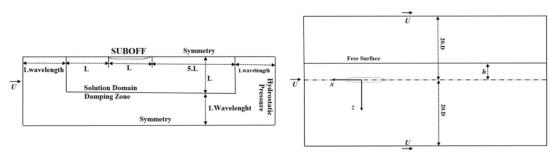
图 6 潜艇水面附近自航计算域示意图(h> 0:水下,h<0:水上)
其中波长的计算可以由以下公式计算得出,当Fr=0.462,L=4.356m时,计算得到的波长λ=5.842m。
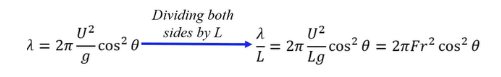
由于仅找到了裸艇体在水面下自航时的实验数据,因此以裸艇体模型展开计算与实验进行对比,表3给出了计算值与实验值的结果对比,计算值较实验值吻合较好,计算值偏小约7%。图7给出了对应的自由液面位置云图。
表 3 计算值与实验值的结果对比(裸艇体)


图 7 自由液面位置云图(水下)
同样的,采用相同的方式对全附体模型建模,计算其水面上自由航行情况下的自由液面位置如下图 8所示。
.png)
图 8 自由液面位置云图(水上)
参考文献
[1] Roddy, R.F. Investigation of the Stability and Control Characteristics of Several Configurations of the DARPA SUBOFFModel (DTRC Model. 5470) from Captive-Model Experiments; David Taylor Research Center Bethesda MDShipHydromechanics Dept: Annapolis, MD, USA, 1990.
[2] Hinze, J. Turbulence; McGraw-Hill Publishing Co.: New York, NY, USA, 1975.

官方微信

扫码关注