堆积问题在生活中随处可见，人们试图寻找可以在最小空间内堆放更多物品的方式，因而最密堆积问题在很早之前就引起了数学家和物理学家的思考。

早在1611年，著名的天体物理学家开普勒关于球体最密堆积方式的猜想就已被提出。按照开普勒猜想，对于大小相等球体，在所有堆积方式中“面心立方最密堆积”和“六方最密堆积”是最密集的堆积方式，二维空间堆积密度为

但这样的结果在当时并没有详细的证明以说明其正确性。

直到1998年，匹兹堡大学数学系教授托马斯·黑尔斯利用计算机辅助方法来排除不同的可能配置，给出了针对开普勒猜想的为裁判小组所接受的证明。这样的证明成为了数学史上的一个里程碑，也标志着计算机在验证复杂数学问题上的一个重大进步。

随着堆积问题研究的不断深入，相关问题的研究引发了越来越多的国内外课题组的广泛关注。2012年第一届“堆积问题国际会议”在爱尔兰都柏林圣三一大学成功举行，吸引了国际上几十个国家的学者前来参加。之后2014年第二届会议在德国埃朗根、2016年第三届会议在中国上海、2019年第四届会议在美国耶鲁大学相继举办，极大促进了堆积问题的研究和发展。

堆积问题是研究晶体结构、液体结构、非均匀材料结构等凝聚态物质系统的重要模型。除了单分散颗粒外，多分散颗粒的密堆积在实际应用中更加广泛。颗粒体系在不同颗粒直径分散性下会表现出不同的密堆积填料分数，这就带来了颗粒级配问题。

在各类工业领域，颗粒材料的级配对于产品的性能有着至关重要的影响。优化颗粒级配以达到紧密堆积，不仅可以提高产品的强度和耐久性，还能显著降低成本。例如：

• 在混凝土砂石骨料中，通过优化粗细砂和碎石的级配，可以提高砂浆的密实度和混凝土性能。

• 在金属粉末冶金和3D打印领域，金属颗粒的级配对材料致密度和力学性能有重要影响。

• 塑料颗粒在注塑成型和挤出成型过程中，合理的级配可以提高产品的表面质量和力学性能。

• 在玻璃纤维、碳纤维等填充材料中，需根据产品要求调整短纤维和长纤维的比例，以达到最佳的材料强度和韧性。

颗粒、粉料的级配通常依赖经验或者实验手段解决，但以经验或实验形成的级配方案并不一定是最优方案，且在材料、粒径多样的情况下会带来高昂的实验成本。采用计算机仿真手段，可以有效辅助优化颗粒级配模型，降低实验成本，缩短产品开发周期。

基于介尺度结构的粗粒化模型

与传统粗粒化方法相比，DEMms的EMMS-DPM 方法在保证精度的同时，极大减少计算量，提高计算效率。

宽粒径分布优化

在处理宽粒径分布的颗粒体系时，DEMms采用多重网格搜索和多重通讯算法，能够优化计算过程，内存使用量降低一个量级，计算速度提升30%。

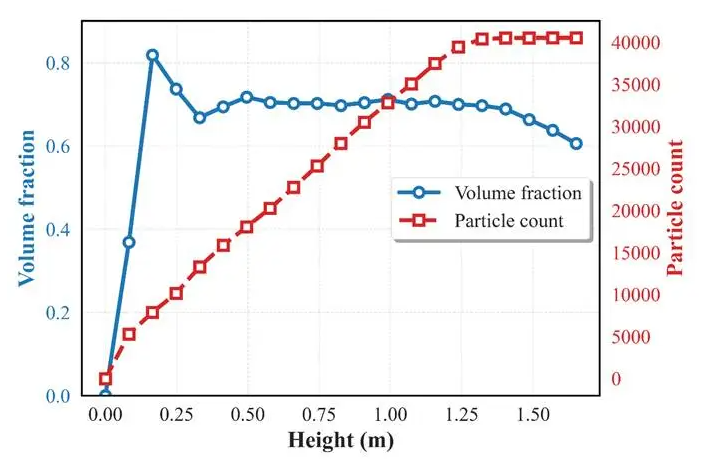
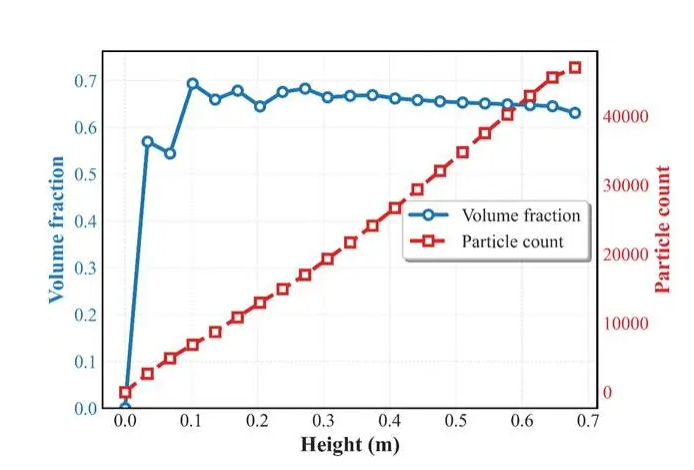
采用DEMms软件，根据不同的颗粒配比输入，可有效模拟颗粒堆积状态，获得颗粒体积分数，助力工程技术人员在多种级配方案中快速筛选优化方案。软件模拟多种不同粒径组合的结果与实验实测的平均体积分数误差小于2%。